Support Vector Machines

Edit me

Overview

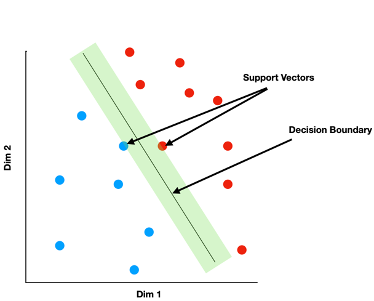
Support Vector Machines (SVMs) are models for binary classification. Suppose you have a dataset of i items, each characterized by values along j feature dimensions, and each belonging to one of two mutually exclusive categories, A or B. Each item i can be considered a point in a continuous feature space of dimension j. SVMs seek a plane in the feature space that does a good job separating all of the A items from all of the B items. The method differs from other approaches to binary classification (such as logistic regression or naive Bayes) in how it defines the best such plane. Specifically, SVM finds the plane that has the largest margin: the “gap” from the classification plane to the closest items in each category is maximized. Only the points nearest the decision plane “matter” for the model fit—the distance between the plane and all other data points is ignored.

The kernel trick

While standard SVMs learn linear classification planes, they can be made to learn nonlinear boundaries through use of the “kernel trick.” The key idea is to enrich the feature data by applying one or more transformations to the raw values on each dimension, then using these transformed values as additional feature dimensions. For instance, if the original data contain feature a, b and c, one can generate three new features by squaring each value to get (a², b², c²). Each item is now situated in a 6-dimensional space rather than a 3-dimensional space, and two categories that were not linearly separable in the original space may be linearly separable in the higher-dimensional space. Thus one can apply a standard SVM in the higher-dimensional space to find the best plane. Moreover, a decision plane that is linear in the higher-dimension space will appear non-linear when back-transformed to the original space. Since the higher-dimension data are just functions of the original data, this amounts to learning a nonlinear boundary in the original space.

Squaring is just one kind of transformation or kernel—many other are possible, and different kernels can be used in combination. For instance, imagine adding the square of each native feature, the cube of each feature, and the sine of each feature. Now the original 3D data reside in a 12D space, and any linear plane in 12D will appear highly nonlinear in the original 3D space. From this example it is clear SVMs and kernel methods can learn highly complex classifications for labeled data, so to guard against over-fitting, it is important to use correct cross-validation techniques.

When are they useful?

SVMs deployed with the kernel trick are especially useful for classification problems with nonlinear decision boundaries in the native data space. They are a great tool to use when you don’t have large datasets, which neural networks usually require, and some non-trivial decision boundary between data points. It is easiest to use SVMs as binary classifiers, though it is possible to generalize to multinomial cases with some modifications. If you have tried linear classifiers and it looks like there is nothing there, why not try a kernel-based SVM? Again, just make sure you are doing proper cross-validation.

Some common examples of SVMs in research on human behavior include:

1. Document/text classification
2. Decoding neural states in functional brain imaging
3. Emotion recognition/classification from visual images
4. Automatic diagnosis of disorders from cognitive/behavioral provides

…and many more.

Recommended Path for Learning

• Patrick Winston’s lecture on SVMs is one of the easiest to follow and assumes a very minimal background in linear algebra and multivariable calculus.

• To get a stronger grasp on the mathematics behind SVMs and do some ‘hands-on’ work with them we recommend this site: Welcome to SVM tutorial - SVM Tutorial.

There are sections that detail different mathematical tools that SVMs employ and there’s a nice R tutorial on doing text-classification using SVMs.

Further Learning

Videos

• One might like Andrew Ng’s lecture on the same from 2018, which is a bit more recent, but SVMs haven’t changed much over the past decade (begins at 46:22).

Code Implementations

• This is a blogpost that walks us through how we might implement SVMs using python’s scikit-learn machine learning package. Guide to implementing SVM and Kernel SVM with Python’s Scikit-Learn.

• Here’s another jupyter notebook based python implementation of SVMs using scikit-learn: SVM using Scikit-Learn in Python.

• This is a jupyter notebook that describes kernel methods that are useful in SVMs and RVMs (relational vector machines). This is a companion to chapter 7 of Bishop’s textbook, Pattern Recognition and Machine Learning. I recommend reading the chapter while looking at this codebase. Jupyter notebook showcasing Kernel methods

Blogs

This blog post is a nice overview that starts with easy intuitions and walks through the hairy-looking mathematical underpinnings with nice geometric interpretations:

• Support Vector Machines.

Papers

Here are 2 papers that employ SVMs in NLP and cognitive neuroscience settings:

• Shallow Semantic Parsing using Support Vector Machines.

• Effective functional mapping of fMRI data with support-vector machines.

• This is a paper that describes how to do functional mapping of fMRI data using support vector machines. Good example of how this method can be used to find temporal or spatial structure in neural data. Effective Functional Mapping of fMRI Data with Support-Vector Machines